谈角膜生物力学，你该有这样的基础

角膜是人眼球屈光系统的重要组成部分, 占眼光学系统屈光力的 2/3以上, 其力学性能对角膜形状的维持、屈光手术的设计、人工角膜的研发 、角膜接触镜的设计等方面有重要作用 , 对角膜疾病如圆锥角膜 、角膜变性 、角膜外伤等的诊断与治疗, 改善视力等有重要参考价值。

角膜是生物材料 , 具有非线性、各向异性 、黏弹性 (包括蠕变 、应力松弛和滞后)的生物力学性能 。弹性模量和泊松比是描述生物力学性能的 2个重要指标 。

弹性模量 = 应力 ÷ 应变

应力：物体由于外因而变形时，在物体内各部分之间产生相互作用的内力，单位面积上的内力称为应力

应变：物体在受到外力作用下会产生一定的变形，变形的程度称应变

应变 ε = △L ÷ L0

* 式中L0是变形的前长度，ΔL是其变形后的伸长量

对于线弹性组织, 弹性模量是一定值;但对于生物组织 , 其应力 /应变呈非线性关系 (图 1)；

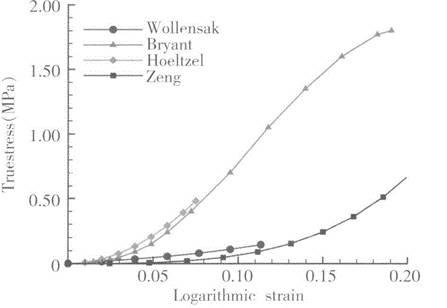
而角膜为非均质材料, 在角膜基质层的不同区域胶原纤维直径不尽相同,角膜的弹性模量不仅与胶原纤维直径有关, 还与年龄、水合状态相关。所以了解角膜生物力学一定要理解粘度，刚度，和滞后。

• 粘度通常被称为流体的“厚度”。例如，蜂蜜的粘度比水高得多。与弹性材料相反，粘性材料在外力作用下不可逆地变形，是在剪切或拉伸应力作用下连续运动，不回复到原来的形状。粘度是其抵抗剪切应力或拉应力渐进变形的一种量度。在分子水平上，粘度是由分子间的相互作用或摩擦引起的。

• 刚度是一个描述物体整体刚度的术语——它是对弹性变形的阻力的测量，是对施加的力的响应。抗弯刚度是抗弯变形的阻力。

刚度 k = F ÷ δ

* 式中F是受外力的合力，δ是其变形量

• 滞后是描述粘弹性材料由于摩擦而引起的能量损失的一个术语。在理想的弹性材料中，就像在理想的弹簧中一样，在弹簧恢复到原来的形状之前不会发生能量损失。因此，这种情况下滞后为零。这个例子说明了滞后受粘性和弹性性质的影响，并不反映硬度或材料刚度

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。纵向应力与纵向应变的比例常数就是材料的弹性模量E，也叫杨氏模量。 而横向应变与纵向应变之比值称为泊松比μ，也叫横向变性系数，它是反映材料横向变形的弹性常数。角膜多被近似认为0.49。

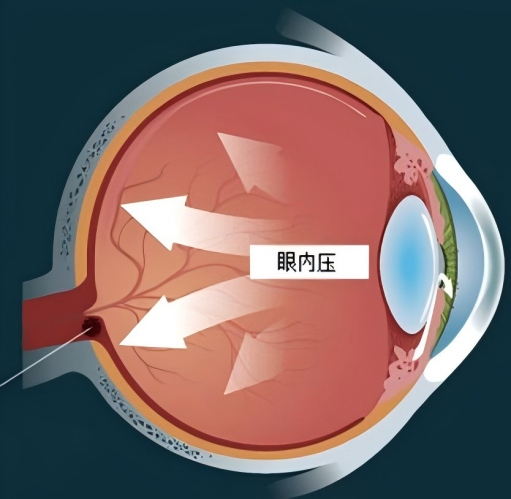
角膜生物力学的另一特色是活体测量的难度，要尽力排除眼内压对于测量结果的影响，这也必须要说一下bIOP,谈一谈有限元分析。有限元分析就是把曲面抽象成一个个点之间的关系，然后分析点和点之间彼此在受力、位移等情况影响之后的变化，在软件建模后，模拟实际状态开始进行运算求解，因为实际问题被较简单的问题所代替，所以这个解不是准确解，而是近似解，可知的变量越多，结果越贴近现实状态。

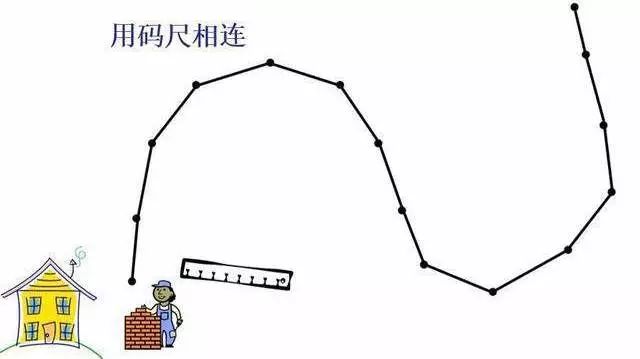
bIOP就是利用了这个算法，参考了角膜生物力学性能等变量得到的结果。这使得即使在生物力学性能发生变化的情况下也能准确地估计眼压。在数值模拟中，系统分析了角膜刚度、角膜厚度、角膜曲率和生物力学性能对眼压测量的影响。在此基础上，建立了一个补偿这些影响因素的方程。实验和临床研究证实了bIOP的准确性。尤其是屈光手术后，眼压比传统的眼压测量方法更精确。

提示各位老师关注bIOP的原因在于，活体测量角膜生物力学，只有排除眼内压的影响，才能获取纯粹的角膜生物力学参数，二者是相辅相成的，眼内压准确，生物力学参数才会准确。

参考文献：

Changes in biomechanically corrected intraocular pressure and dynamic corneal response parameters before and after transepithelial photorefractive keratectomy and femtosecond laser–assisted laser in situ keratomileusis: Journal of Cataract & Refractive Surgery 43 (12), 2017: 1495 -1503.

NashIS,GrenePR,FosterCS.Comparison of mechanical proper ties of keratoconus and normal corneas[ J] .ExpEyeRes,  1982, 35 (5 )∶413 -424

ElsheikhA, WangD, BrownM, etal.Asesmentof corneal biomechanical proper ties and their variation with age[ J] .CurEyeRes, 2007, 32(1)∶11 -19

角膜生物力学性能测量方法的研究进展   姜  黎   综述       王勤美   曾衍钧   审校  分类号       R772.2    文献标识码 A 文章编号 1003-0808(2009)09-0824-05

王元，文兰，陈木法．数学大辞典：科学出版社，2010